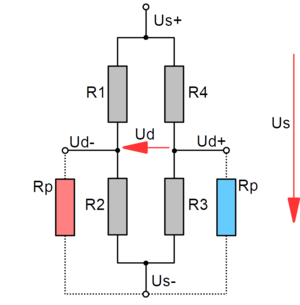
Nichtlinearität der Brückenschaltung
Bei der Berechnung des Shuntwiderstands in Gleichung 5 wurde die linearisierte Form der Brückengleichung verwendet:
ΔUd/Us = 1/4 (ΔR1/R1 - ΔR2/R2 + ΔR3/R3 - ΔR4/R4) (Gl. 6)
bzw. für die Viertelbrücke mit nur einem aktiven DMS R1 mit R = R1 = R2 = R3 = R4
ΔUd/Us = 1/4 (ΔR/R) (Gl. 7)
Die exakte Lösung für die Viertelbrücke lautet: (aus wheatstone-bruecke.pdf)
Ud/Us = 1/4 (ΔR/R) · 1/ (1 + ΔR/2R) (Gl. 8)
Der zusätzliche Term 1/(1 + ΔR/2R) berücksichtigt den nichtlinearen Anteil.
bzw. mit c = 1/(1 - 2·ΔUd/Us) und Gl. 4 und aufgelöst nach Rp (aus wheatstone-bruecke.pdf):
Rp = R · (1/4 · 1/Ud/Us - 1) · 1/c (Gl. 9)
Die mit der linearisierten Brückengleichung berechnete Brückenverstimmung ist um den Faktor c zu groß.
Bei einer linearisiert berechneten Dehnung von 1000 µm/m beträgt die exakte Dehnung 999 µm/m. Der Fehler ist ca. +1 µm/m (+0,1 %).
Mit 87150 Ohm parallel zu einem 350 Ohm DMS wird die Brücke um 0,998 mV/V verstimmt.Dies entspricht einer Dehnung von 2000 µm/m bei einem k-Faktor von 2.
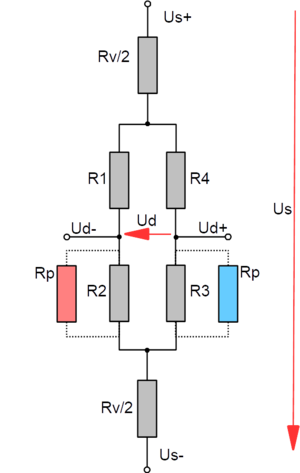
Ein weiterer Fehler entsteht durch zusätzliche Vorwiderstände. Dies können z.B. die Widerstände von Zuleitungen sein, oder für den Normsignalabgleich von Sensoren eingebaute Kalibrierwiderstände, und für den Abgleich der Drift des E-Moduls eingebaute temperaturabhängige Nickel- Widerstände. Das Schaltbild der Wheatstone'schen Brücke mit Vorwiderständen zeigt die folgende Abbildung.
Brückenschaltung mit Vorwiderstand