Grundlagen zur Wheatstone'schen Brückenschaltung
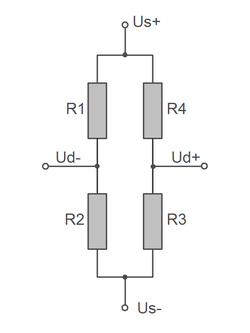 |
Die zwei Anschlüsse Us+ und Us- dienen der Speisung der Brückenschaltung. Us- Die Spannung zwischen Us+ und Us- wird auch als Brückenspeisespannung Us oder Brückenspeisung oder Sensor-Eingang bezeichnet. Us- ist bei den vielen Messverstärkern mit der Masse GND verbunden. |
Über die Anschlüsse Ud+ und Ud- wird die Spannungsänderung gemessen, wenn die Brückenschaltung infolge Dehnung an einem oder mehreren DMS verstimmt wird.
Die Spannung zwischen Ud+ und Ud- wird als "Differenzspannung Ud" oder "Brückenausgang" oder als "Sensor-Ausgang" bezeichnet.
Die Brückenschaltung ist abgeglichen (die Spannung zwischen Ud+ und Ud- ist 0 V), wenn die folgende Bedingung erfüllt ist:
Meist wird die Brückenschaltung mit Gleichspannung von 5V gespeist. Üblich sind auch 2,5V Brückenspeisung oder 1,0V Brückenspeisung, wenn z.B. ein niederohmiger Dehnungsmessstreifen (DMS) mit 120 Ohm eingesetzt wird, oder wenn der DMS auf ein nichtleitendes Material geklebt wird, so dass eine starke Eigenerwärmung des Dehnungsmessstreifens verhindert werden muss.
