Shunt calibration

Zero adjustment and function test with shunt resistor

By connecting a resistor Rp in parallel to a strain gauge, a defined detuning of the measuring bridge can be achieved. This can be used for a functional test. Alternatively, this method can also be used to adjust the output signal of the Wheatstone bridge to 0 mV.

To do this, the shunt resistor is permanently inserted into the strain gauge bridge circuit, or alternatively into the connection terminals of the measuring amplifier.

By connecting a shunt resistor Rp in parallel to one of the four bridge resistors R, a resistance change ΔR results:

Converted as a relative resistance change, we get:

With the bridge equation for the DMS quarter bridge

Inserting equation 3 into equation 2, we get:

and transformed to Rp:

Rp = R · (1/4 · 1/Ud/Us  -  1)      (eq. 5)

Shunt resistors for 350 Ohm strain gauges

Shunt resistors for 120 Ohm strain gauges

Shunt resistors for 1000 Ohm strain gauges

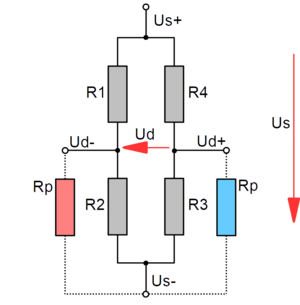
Nonlinearity of the bridge circuit

When calculating the shunt resistance in Equation 5, the linearized form of the bridge equation was used:

or for the quarter bridge with only one active strain gauge R1 with R = R1 = R2 = R3 = R4

The exact solution for the quarter bridge is: (from wheatstone-bridge_en.pdf)

The additional term 1/(1 + ΔR/2R) takes the nonlinear component into account.

or with c = 1/(1 -  2·ΔUd/Us)  and eq. 4 nd solved for Rp (from wheatstone-bridge_en.pdf):

The bridge detuning calculated with the linearized bridge equation is too large by a factor of c. 

With a linearized calculated strain of 1000 µm/m, the exact strain is 999 µm/m. The error is approximately +1 µm/m (+0.1%).

With 87150 ohm in parallel with a 350 ohm strain gauge, the bridge is detuned by 0.998 mV/V. This corresponds to a strain of 2000 µm/m at a k-factor of 2.

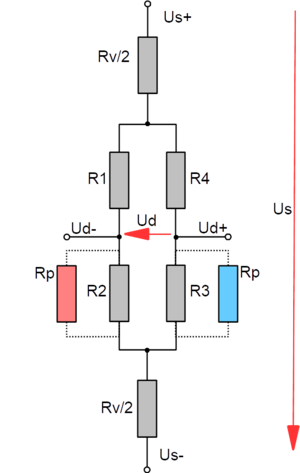
Another error is caused by additional series resistors. These can be, for example, the resistance of supply lines, or calibration resistors built in for the standard signal adjustment of sensors, and temperature-dependent nickel resistors built in for the drift adjustment of the E-module. The circuit diagram of the Wheatstone bridge with series resistors is shown in the following figure.

Bridge circuit with series resistor

Rv is composed, for example, of 2x 1 Ohm line resistance plus 2x 20 Ohm nickel series resistors plus 2x 10 Ohm fixed resistors = 62 Ohms. Considering the additional voltage divider, which leads to a reduction in the supply voltage Us at the Wheatstone bridge, the bridge equation of the quarter bridge (with R = R1 = R2 = R3 = R4) is:

or c = 1/(1 -  2·ΔUd/Us) and eq. 4 and eq. 10 solved for Rp:

The red parts take into account the nonlinearity of the bridge circuit, the blue parts take into account the influence of the series resistors.