Definition and measurement of resolution
Definition of SNR in logarithmic scale (dB)
An important criterion for the quality of measured values is the resolution. The resolution can be defined or characterized in different ways.
One way to characterize the resolution is to specify the signal-to-noise ratio (SNR or S/N). The signal-to-noise ratio is defined as the ratio of the signal powers:
SNR =PSignal /PNoise
As the useful signal power is usually several orders of magnitude higher than the noise power, a logarithmic scale is used. The resulting measure is called decibel (dB). As the power “P” is proportional to the square of the electrical voltages “u”, the following relationship applies:
Definition of SNR on a linear scale
Another definition, which is particularly common in optical measurement technology, describes the ratio of the useful signal amplitude uSignal to the standard deviation S of the noise signal amplitude uNoise
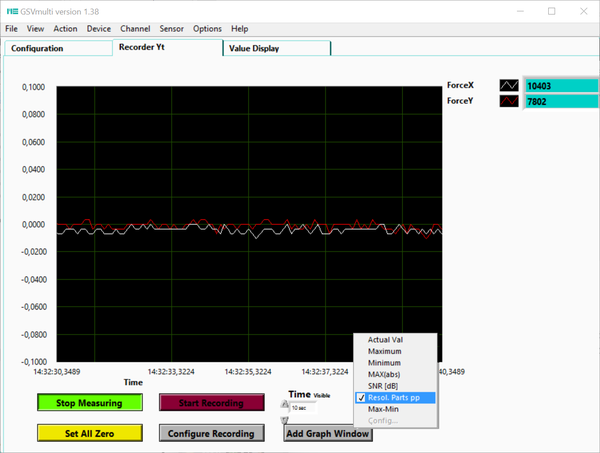
Division of the measurement range into “number of peak amplitudes”
A clear measure of resolution is obtained by dividing the measurement range by the noise amplitude. A particularly strict definition is that the peak amplitude of the noise is used instead of the standard deviation of the noise amplitude:
Number of peak amplitudes = measuring range / noise amplitude
The measuring range of 2 mV/V should consist of at least 10,000 parts of the peak value amplitude. With very good amplifiers, a factor of 100,000 and more can also be achieved.
The noise amplitude, measured as the peak amplitude of the last 100 measured values, is then less than 20 nV/V.
In the GSVmulti software, this method is called “Resol. Parts. pp” in the GSVmulti software.