Call Us
The application of the Wheatstone bridge circuit offers three main advantages:
By using a total of 4 measuring grids and suitable wiring, the output signal can be increased compared to the use of a single measuring grid.
Grids R1 and R3 are arranged on the top of the bending beam, grids R2 and R4 are arranged on the bottom of the beam. Temperature-related strain and strain due to axial force or torsion are compensated in this circuit. Only the bending around one axis is recorded.
The mechanical stress results from the beam height h, the beam width b (the section modulus Wb = bh²/6 for a rectangular cross-section),
and from the bending moment (Mb = F L) from the force F and the lever arm L:
Using Hooke's law σ = E · ε and the bridge equation (5b) for strain gauges and the section modulus Wb we obtain for the bending beam with rectangular cross-section:
To measure the bending, strain gauges with two parallel grids are used:
 |
In the circuit for axial force, the strain gauges are arranged so that the longitudinal and transverse strains are measured. In contrast to the bending beam, the measuring grids R2 and R4 only contribute approx. 30% of the signal from the measuring grids R1 and R3. They contribute the same amount to the output signal: The following applies to the change in resistance at R2: ΔR2/R2 = -ν ΔR1/R1.
Temperature-related expansion and expansion due to bending or torsion are compensated in this circuit. Only the axial force is recorded.
The mechanical stress results from the force F and the cross-sectional area A = b h:
σ = F / A
To measure the axial force, strain gauges with two mutually perpendicular grids (T-rosette) are used:
 |
The connection between grid R1 and R2 or R3 and R4 can already be made on the DMS carrier, so that only 3 soldering surfaces are required.
To compensate for the bending around the vertical axis, a small distance between the grids R1-R2 and R3-R4 is required.
For small dimensions, an installation of one grille per side surface, or an installation of a T-rosette per side surface with a series connection of two grilles is recommended.
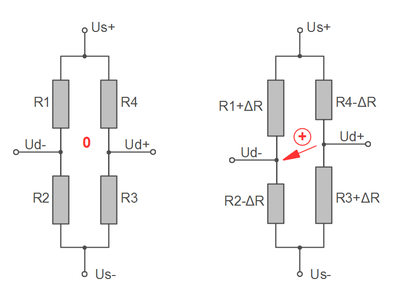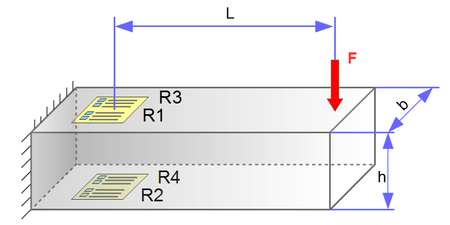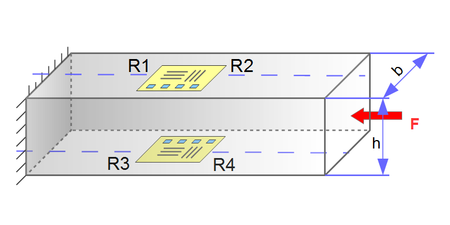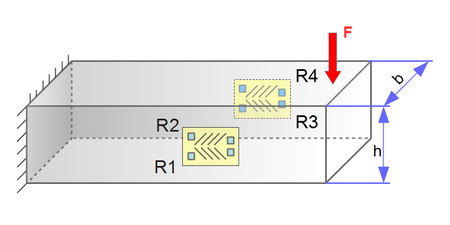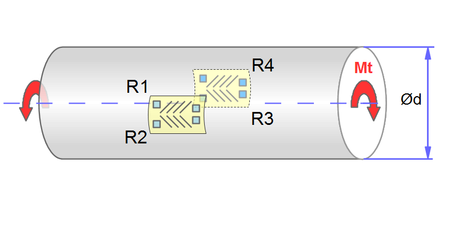
The maximum strain in a torsion bar is less than 45° to the shaft axis. By arranging two measuring grids at +45° and -45°, a bridge circuit with two positively and two negatively strained grids can be realized, similar to the bending stress.
Grid R1 is parallel to grid R3 and positively stretched at right-hand moment.
Grid R2 is parallel to grid R4 and negatively stretched ("compressed") at right-hand moment.
Temperature-related expansion and expansion due to bending or axial force are compensated for with this circuit. Only the torsion is recorded.
The mechanical stress σt results from the torsional moment Mt and the section modulus Wt against torsion:
The following applies to the solid cylinder:
The following applies to the hollow shaft:
Further information in: kb-festigkeitslehre.pdf
To measure the torsion, strain gauges with a +45/-45 grid arrangement are used.
The connection between grid R1 and R2 or R3 and R4 can already be made on the strain gauge carrier, so that only 3 soldering surfaces are required.
A simplified installation, especially for shafts with large diameters (e.g. ship shafts, generator drive shafts) is possible by using a strain gauge full bridge 4x45°
In the case of inhomogeneous stress curves, for example when installing strain gauges at a short distance from splines, the installation of 4 measuring grids on the circumference or 4 double grids in series is recommended.
 |
 |
 |
The maximum strains in a shear bar are below 45° in the region of the neutral fiber.
By arranging two measuring grids at +45° and -45°, a bridge circuit with two positively and two negatively stretched grids can be realized, similar to the bending and torsional stress.
Grid R1 and grid R3 are positively stretched.
Grid R2 and Grid R4 are negatively stretched (“compressed”).
Temperature-related expansion and stretching due to bending, axial force or torsion are compensated for with this circuit. Only the shear is recorded
The mechanical stress σt results from the force F and the cross section A=b h
σ ≈ F / A * 1,4
To measure shear, strain gauges with a +45/-45 grid arrangement are used (as for torsion).